Os sistemas de projeções cartográficas foram desenvolvidos
para dar uma solução ao problema da transferência
de uma imagem da superfície curva da esfera terrestre para um
plano da carta, o que sempre vai acarretar deformações.
Os sistemas de projeções constituem-se de uma fórmula
matemática que transforma as coordenadas geográficas, a
partir de uma superfície esférica (elipsoidal), em coordenadas
planas, mantendo correspondência entre elas. O uso deste artifício
geométrico das projeções consegue reduzir as deformações,
mas nunca eliminá-las.
Os tipos de propriedades geométricas que caracterizam as projeções cartográficas, em suas relações entre a esfera (Terra) e um plano, que é o mapa, são:
a) Conformes – os ângulos são mantidos idênticos (na esfera e no plano) e as áreas são deformadas.
b) Equivalentes – quando as áreas apresentam-se idênticas e os ângulos deformados.
c) Afiláticas – quando as áreas e os ângulos apresentam-se deformados.
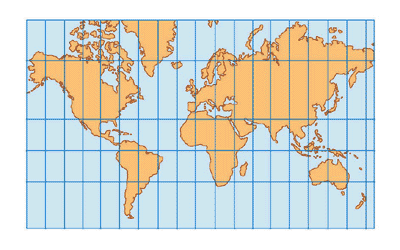
Projeção de Mercator
Nesta projeção os meridianos e os paralelos são linhas retas que se cortam em ângulos retos. Corresponde a um tipo cilíndrico pouco modificado. Nela as regiões polares aparecem muito exageradas.
Projeção de Peters
Outra projeção muito utilizada para planisférios é a de Arno Peters, que data de 1973. Sua base também é cilíndrica equivalente, e determina uma distribuição dos paralelos com intervalos decrescentes desde o Equador até os pólos, como podemos observar no mapa a seguir.
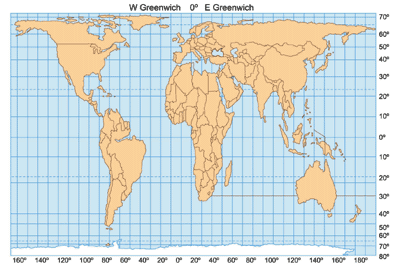
As retas perpendiculares aos paralelos e as linhas meridianas têm intervalos menores, resultando na representação das massas continentais, um significativo achatamento no sentido Leste-Oeste e a deformação no sentido Norte-Sul, na faixa compreendida entre os paralelos 60o Norte e Sul, e acima destes até os pólos, a impressão de alongamento da Terra
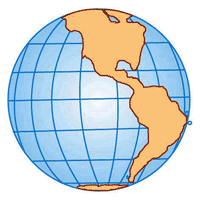
Projeção ortográfica
Ela nos apresenta um hemisfério como se o víssemos a grande distância. Os paralelos mantêm seu paralelismo e os meridianos passam pelos pólos, como ocorre na esfera. As terras próximas ao Equador aparecem com forma e áreas corretas, mas os pólos apresentam maior deformação.
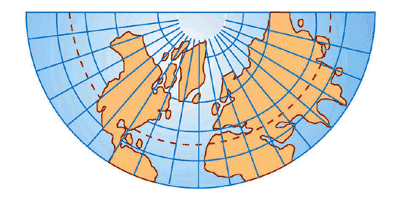
Projeção cônica
Nesta projeção os meridianos convergem para os pólos e os paralelos são arcos concêntricos situados a igual distância uns dos outros. São utilizados para mapas de países de latitudes médias.
Projeção de Mollweide
Nesta projeção os paralelos são linhas retas e os meridianos, linhas curvas. Sua área é proporcional à da esfera terrestre, tendo a forma elíptica. As zonas centrais apresentam grande exatidão, tanto em área como em configuração, mas as extremidades apresentam grandes distorções.
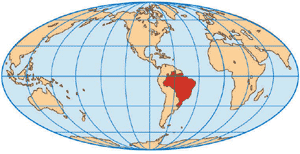
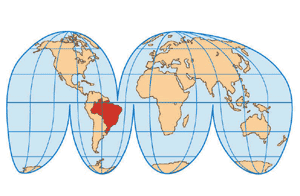
Projeção de Goode, que modifica a de Moolweide
É uma projeção descontínua, pois tenta eliminar várias áreas oceânicas. Goode coloca os meridianos centrais da projeção correspondendo aos meridianos quase centrais dos continentes para lograr maior exatidão.
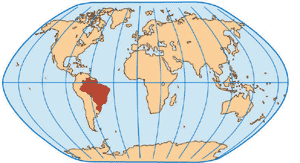
Projeção de Holzel
Projeção equivalente, seu contorno elipsoidal faz referência à forma aproximada da Terra que tem um ligeiro achatamento nos pólos.
Projeção Azimutal
Equidistante Oblíqua Centrada na Cidade de São Paulo
Nesta projeção, centrada em São Paulo, os ângulos azimutais são mantidos a partir da parte central da projeção.
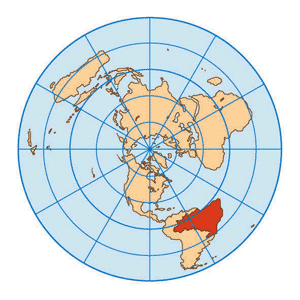
Projeção Azimutal Equidistante Polar
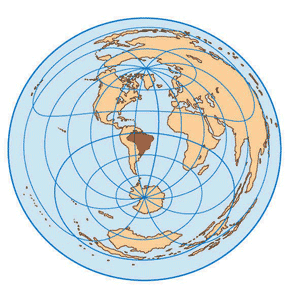
Projeção equidistante que tem os pólos em sua porção central. As maiores deformações estão em suas áreas periféricas.

