Álgebra

Função exponencial e função logarítmica

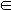
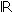
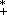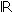
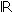
1. A função exponencial de base a, com a - {1}, é a função f : 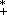definida por f(x) = a^x.
   
2. Se N > 0, a > 0 e a ≠ 1, então:
   Log_aN = α <=> a^α = N
   
3. A função logaritmica de base a, com a - {1}, é a função g : definida por g(x) = log_ax.
4. Sendo a > 0, a ≠ 1, m > 0 e n > 0, tem-se:
   
   • log_a(m.n) = log_am + log_an
   • log_a(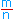) = log_am - log_an
   • log_a(mⁿ) = n . log_am
   • log_am = 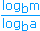. com b > o e b ≠ 1
     
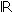
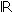
5. A função exponencial de 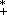e a função logarítmica de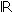 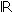são inversas uma da outra.
   
6. Seus gráficos, representados abaixo, são simétricos em relação à bissetriz dos qadrados impares, que é a reta de equação y = x.
   
   
   
   
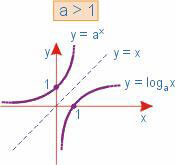
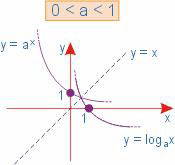
7. A função exponencial e a função logarítmica dão injetoras, pois qualquer reta horizontal intercepta o gráfico no máximo uma vez. Logo:
   a^x1 = a^x2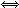 x₁ = x₂
   log_ax₁ = log_ax₂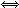 x₁ = x₂ > 0
   
8. Se a > 1, as funções são, ambas, estritamente crescentes e, portanto,
   a^x1 > a^x2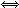 x₁ > x₂
   log_ax₁ > log_ax₂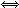 x₁ > x₂ > 0
   
   
9. Se 0 < a < 1, as funções são, ambas, estritamente decrescentes e, portanto,
   a^x1 > a^x2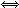 x₁ < x₂
   log_ax₁ > log_ax₂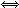 0 < x₁ < x₂